Circunferencia

La circunferencia es una línea curva, plana y cerrada. La definición más gradual de este concepto es:

A la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos distintos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir,esta la circunferencia es el perímetro del círculo cuya superficie contiene un circulo

Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.

La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica.

Elementos de la circunferencia

Secantes, cuerdas y tangentes.

La mediatriz de una cuerda pasa por el centro de la circunferencia.

Existen varios puntos, rectas y segmentos, singulares en la circunferencia:

• Centro, el punto interior equidistante de todos los puntos de la circunferencia;
• Radio, el segmento que une el centro con un punto cualquiera de la circunferencia;
• Diámetro, el mayor segmento que une dos puntos de la circunferencia (necesariamente pasa por el centro);
• Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros)
• Recta Secante, la que corta a la circunferencia en dos puntos;
• Recta Tangente o simplemente Tangente, la que toca a la circunferencia en un sólo punto;
• Punto de tangencia, el de contacto de la recta tangente con la circunferencia;
• Arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia;
• Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.

Posiciones relativas

La circunferencia y un punto

Un punto en el plano puede ser:

• Exterior a la circunferencia, si la distancia del centro al punto es mayor que la longitud del radio.
• Perteneciente a la circunferencia, si la distancia del centro al punto es igual a la longitud del radio.
• Interior a la circunferencia, si la distancia del centro al punto es menor a la longitud del radio.

La circunferencia y la recta

Una recta, respecto de una circunferencia, puede ser:

• Exterior, si no tienen ningún punto en común con ella y la distancia del centro a la recta es mayor que la longitud del radio.

• Tangente, si la toca en un punto (el punto de tangencia o tangente) y la distancia del centro a la recta es igual a la longitud del radio. Una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro.

• Secante, si tiene dos puntos comunes, es decir, si la corta en dos puntos distintos y la distancia del centro a la recta es menor a la longitud del radio.Cuerda que pasa por el centro de la circunferencia

• Segmento circular, es el conjunto de puntos de la región circular comprendida entre una cuerda y el arco correspondiente

Dos circunferencias

Dos circunferencias, en función de sus posiciones relativas, se denominan:

• Exteriores, si no tienen puntos comunes y la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 1)

• Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. La distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 2)

• Secantes, si se cortan en dos puntos distintos y la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos. Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto. (Figura 3)

• Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. La distancia que hay entre sus centros es igual al valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra. (Figura 4)

• Interiores excéntricas, si no tienen ningún punto común y la distancia entre sus centros es mayor que 0 y menor que el valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.

• Interiores concéntricas, si tienen el mismo centro (la distancia entre sus centros es 0) y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. (Figura 5)

• Coincidentes, si tienen el mismo centro y el mismo radio. Si dos circunferencias tienen más de dos puntos comunes, necesariamente son circunferencias coincidentes.

Ángulos en una circunferencia

Ángulos en la circunferencia.

Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.

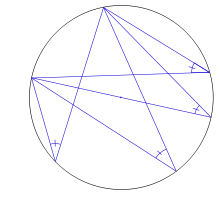
Un ángulo, respecto de una circunferencia, pueden ser:

Ángulo central, si tiene su vértice en el centro de esta. Sus lados contienen a dos radios.

La amplitud de un ángulo central es igual a la del arco que abarca.

Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.

La amplitud de un ángulo inscrito en una semi circunferencia equivale a la mayor parte del ángulo exterior que limita dicha base. (Véase: arco capaz.)

Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.

La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.

Ángulo interior, si su vértice está en el interior de la circunferencia.

La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.

Ángulo exterior, si tiene su vértice en el exterior de la circunferencia

Longitud de la circunferencia

La longitud $\ell$ de una circunferencia es:

$\ell =\pi \cdot 2r$

donde $r\,$ es la longitud del radio.

Pues $\pi \,$ (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:

$\pi ={\frac {\ell }{2r}}$

Área del círculo delimitado por una circunferencia

Área del círculo = π × área del cuadrado sombreado.

El área del círculo delimitado por la circunferencia es:

$A=\pi \cdot r^{2}$

Ecuaciones de la circunferencia

Ecuación en coordenadas cartesianas

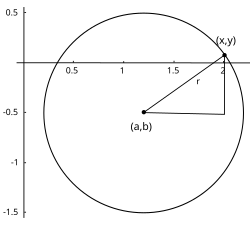
En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación

$(x-a)^{2}+(y-b)^{2}=r^{2}\,$.

Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al

$x^{2}+y^{2}=r^{2}\,$.

La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.

De la ecuación general de una circunferencia,

$(x-a)^{2}+(y-b)^{2}=r^{2}\,$

se deduce:

$x^{2}+y^{2}+Dx+Ey+F=0\,$

resultando:

$a=-{\frac {D}{2}}$

$b=-{\frac {E}{2}}$

$r={\sqrt {a^{2}+b^{2}-F}}$

Si conocemos los puntos extremos de un diámetro: $(x_{1},y_{1}),(x_{2},y_{2})\,$,

la ecuación de la circunferencia es:

$(x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0.\,$

Ecuación vectorial de la circunferencia

La circunferencia con centro en el origen y radio R, tiene por ecuación vectorial: ${\vec {r}}\ =\langle R\cos(\theta ),R\sin(\theta )\rangle \,$. Donde $\theta \,$ es el parámetro de la curva, además cabe destacar que $\theta \in [0,2\pi )$. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.

Ecuación en coordenadas polares

Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como $(r,\theta )\,$

$r=c.\,$

Cuando el centro no está en el origen, sino en el punto $(s,\alpha )\,$ y el radio es $c\,$, la ecuación se transforma en:

$r^{2}-2sr\,\cos(\theta -\alpha )+s^{2}=c^{2}$

Ecuación en coordenadas paramétricas

La circunferencia con centro en (a, b) y radio c se parametriza con funciones trigonométricas como:

$x=a+c\cos t,\ y=b+c\sin t,\qquad t\in [0,2\pi ]$

y con funciones racionales como

$x=a+c\left({\frac {1-t^{2}}{1+t^{2}}}\right),\ y=b+c\left({\frac {2t}{1+t^{2}}}\right),\qquad -\infty \leq t\leq \infty$

Circunferencia en topología

En topología, se denomina circunferencia a cualquier curva cerrada que sea homeomorfa a la circunferencia usual de la geometría (es decir, la esfera 1–dimensional). Se la puede definir como el espacio cociente determinado al identificar los dos extremos de un intervalo cerrado.

Los geómetras llaman 3-esfera a la superficie de la esfera. Los topólogos se refieren a ella como 2-esfera y la indican como $S^{2}\;$.

Circunferencia en un plano de ejes de referencia no ortogonales

Plano oblicuo, Construcción de la Circunferencia.

Para construir una circunferencia en el plano oblicuo, no se puede usar la misma ecuación que se usa en un plano ortogonal, por lo que es necesario introducir algunos conceptos que nos ayudarán a entender la construcción de tal ecuación. Tales conceptos son los de trigonometría.

Se debe tener presente que en este plano una ecuación de circunferencia se llamará así si se ve como tal. Es por esta razón que se descarta la ecuación anterior, porque en el plano oblicuo no parecerá circunferencia, sino una elipse.

Construcción de una circunferencia

Usaremos el mismo razonamiento usado anteriormente y nos guiaremos por la figura adjunta. Dijimos que en el plano ortogonal, la ecuación de la circunferencia cumplía con que todos los puntos de la función equidistan de un punto llamado centro de la circunferencia. En este plano, las distancias siguen siendo las mismas, no es un plano en perspectiva, sólo es un plano inclinado, por lo tanto el Teorema de Pitágoras sigue siendo válido si se aplica de manera correcta.

• Razonamiento

${\mathit {d=}}\,\!$ la distancia entre los puntos ${\mathit {A}}\,\!$ y ${\mathit {B}}\,\!$

${\mathit {a=}}\,\!$ la distancia entre los puntos ${\mathit {C}}\,\!$ y ${\mathit {B}}\,\!$, es decir ${\mathit {a=|y_{1}-y_{2}|}}\,\!$

${\mathit {b=}}\,\!$ la distancia entre los puntos ${\mathit {C}}\,\!$ y ${\mathit {A}}\,\!$, es decir, ${\mathit {b=|x_{2}-x_{1}|}}\,\!$.

Por el Teorema del coseno tenemos que la distancia ${\mathit {d}}\,\!$ entre los puntos ${\mathit {A}}\,\!$ y ${\mathit {B}}\,\!$ viene dada por la siguiente relación

${\mathit {d^{2}=a^{2}+b^{2}-2ab\cos {\alpha }}}\,\!$

${\mathit {d^{2}=|y_{1}-y_{2}|^{2}+|x_{2}-x_{1}|^{2}-2|y_{1}-y_{2}||x_{2}-x_{1}|\cos {\alpha }}}\,\!$

luego,

${\mathit {d={\sqrt {|y_{1}-y_{2}|^{2}+|x_{2}-x_{1}|^{2}-2|y_{1}-y_{2}||x_{2}-x_{1}|\cos {\alpha }}}}}\,\!$

Deben destacarse dos cosas en este procedimiento

• Se prescinde del uso del valor absoluto en la raíz. Es un número positivo porque está al cuadrado
• Nótese que si definimos las pendientes negativas para las rectas que intersecan al eje ${\mathit {x}}\,\!$ con un ángulo mayor que ${\mathit {\alpha }}\,\!$, se cumple esta relación. Si el ángulo de intersección con el eje ${\mathit {x}}\,\!$ es menor, el signo menos que acompaña al ${\mathit {2}}\,\!$ será positivo. (se puede demostrar)

Conlcluímos entonces que en esta relación no hay pérdida de generalidad.

Con esta relación, podemos encontrar la ecuación de una circunferencia, basándonos en el hecho de que la distancia desde el centro, hasta cualquier parte de la frontera o borde será la misma. Fijaremos un centro con las coordenadas cartesianas ${\mathit {(h,k)}}\,\!$ (fijo). Así, si ${\mathit {x}}\,\!$ e ${\mathit {y}}\,\!$ varían, todo el conjunto de pares ${\mathit {(x,y)}}\,\!$ para cada ${\mathit {x}}\,\!$ e ${\mathit {y}}\,\!$ reales, formarán la frontera de nuestra circunferencia de centro ${\mathit {(h,k)}}\,\!$.

Luego, si la distancia constante del centro a la cirunferencia la llamamos ${\mathit {r}}\,\!$, podemos decir que ${\mathit {r}}\,\!$ será nuestro radio de circunferencia. Entonces,

${\mathit {r^{2}=|x-h|^{2}+|y-k|^{2}-2|x-h||y-k|\cos {\alpha }}}\,\!$

${\mathit {r^{2}=(x-h)^{2}+(y-k)^{2}-2|x-h||y-k|\cos {\alpha }}}\,\!$

será la ecuación de la circunferencia en un plano con un ángulo de inclinación ${\mathit {\alpha }}\,\!$.

Un caso particular de esta ecuación es cuando ${\mathit {\alpha ={\frac {\pi }{2}}}}\,\!$. En este caso volvemos al plano ortogonal y la ecuación de la circunferencia es la misma que habíamos demostrado. Se puede decir entonces, que la ecuación de la circunferenca en el plano ortogonal es un caso particular de éste.

El área es la misma en este caso, ya que el área sólo está en función del radio y no del ángulo de inclinación del plano al que pertenece.

Otras propiedades

• Potencia de un punto: si dos cuerdas se intersecan, el producto de los segmentos formados en la una, es igual al producto de los segmentos formados en la otra cuerda, $A_{1}P\cdot PB_{1}=A_{2}P\cdot PB_{2}$.

• El segundo teorema de Tales muestra que si los tres vértices de un triángulo están sobre una circunferencia dada, siendo uno de sus lados el diámetro de la circunferencia, entonces, el ángulo opuesto a éste lado es un ángulo recto (véase arco capaz).

Triángulos rectángulos inscritos en una semicircunferencia.

• Dados tres puntos cualesquiera no alineados, existe una única circunferencia que contiene a estos tres puntos (esta circunferencia estará circunscrita al triángulo definido por estos puntos). Dados tres puntos no alineados en el plano cartesiano $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})\,$, la ecuación de la circunferencia está dada de forma simple por la determinante matricial:

$\det {\begin{bmatrix}x&y&x^{2}+y^{2}&1\\x_{1}&y_{1}&x_{1}^{2}+y_{1}^{2}&1\\x_{2}&y_{2}&x_{2}^{2}+y_{2}^{2}&1\\x_{3}&y_{3}&x_{3}^{2}+y_{3}^{2}&1\\\end{bmatrix}}=0.$