Análisis de circuitos: Leyes de Kirchhoff

El análisis de circuitos será la parte central de este tema, para ello sera vital emplear las leyes de kirchhoff asi como los conocimientos adquiridos hasta ahora, y algunos conceptos nuevos.

Circuito explicación leyes de kirchhoff

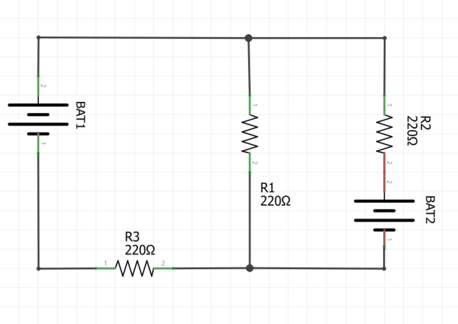
Malla: Se llama malla a una trayectoria cerrada en un circuito eléctrico por el cual fluye una corriente I.

Nodo: Se llama nodo a un punto donde se unen 3 o mas conductores, en la imagen de la derecha vemos dos nodos señalados por un punto en su unión.

1ª Ley de Kirchhoff: Ley de mallas

Esta ley dice lo siguiente:

$\sum _{i}\Delta V_{i}=0$

Es decir que la suma de todas las diferencias de potencial en una malla ha de ser 0. Esta ley es lógica si la pensamos y relacionamos con el apartado anterior de fuerza eléctromotriz, como vimos las fem se empleaban para suplir esas carencias de potencial.

2ª Ley de Kirchhoff: Ley de nodos

Esta ley se aplica sobre los nodos del circuito y enuncia que la suma de todas las intensidades entrantes a un nodo será igual a la suma de las intensidades salientes, matemáticamente:

$\sum _{i}I_{i}=0\Leftrightarrow \sum I.entrantes=\sum I.salientes$

Procedimiento a seguir para el análisis de circuitos

1. Tomar mallas independientes en nuestro circuito.
2. Fijar un sentido arbitrario de la intensidad para cada malla.
3. Aplicar la primera ley de Kirchhoff empleando el criterio de signos para los elementos del circuito en función de las intensidades asignadas a cada malla.
4. Aplicar la segunda ley de Kirchhoff y resolver el sistema generado obteniendo las intensidades buscadas.

La corriente va en el sentido indicado por la flecha

$\Delta V=-\epsilon$	$\Delta V=\epsilon$	$\Delta V=IR$	$\Delta V=-IR$

Así pues, a partir de esta tabla podemos aplicar el procedimiento recién explicado completo, aplicando la 1ª Ley de Kifchhoff obtendremos una serie de ecuaciones que podremos resolver si usamos la 2ª ley para completar nuestro sistema.

Ejercicio 1

Calcular las intensidades que recorren el circuito mostrado en la imagen si R1 = 2 Ω, R2 = 4Ω y R3 = 2Ω con BAT 1 = 6 V y BAT 2 = 4 V.

solución

Proyecto: Física General

Anterior: Fuerza Electromotriz — Análisis de circuitos: Leyes de Kirchhoff — Siguiente: Circuitos RC: Carga y descarga de un condensador