Mecánica cuántica/Historia

Divergencia de la teoría clásica conocida cómo catástrofe ultravioleta

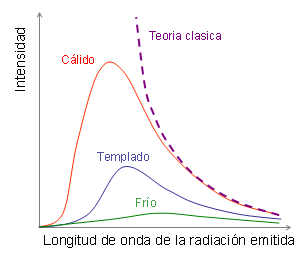
El origen de esta nueva rama de la física, irónicamente, no nace de cuestionamientos mecánicos inicialmente. A inicios del siglo XX, el problema de la radiación de cuerpo negro, perteneciente a la mecánica estadística, estaba resuelto a medias, pues no se descubría una función analítica de distribución de densidad de energía que se ajuste a los resultados experimentales medidos de un cuerpo negro.

Emisión y absorción

Gustav Kirchhoff, desarrollaría un teorema que relaciona la emisión y absorción de un cuerpo, la cual confirma los resultados experimentales de Thomas Wedgwood (familiar de Charles Darwin). Él declara que para todo cuerpo en equilibrio térmico con radiación la potencia de radiación emitida es proporcional a la potencia absorbida:

$e_{\nu }=J(\nu ,T)A_{\nu }$ Ecuación 1

Donde $e_{\nu }$ representa la potencia por unidad de área por unidad de frecuencia (${\frac {W}{m^{2}f}}$), la función $J$ es una función universal (misma para todos los cuerpos) que solo depende de la frecuencia $\nu$ y temperatura su temperatura absoluta $T$. La constante $A_{\nu }$ depende del problema y es la fracción de radiación que es emitida vs la absorbida, toma valores entre el intervalo $[0,1]$. Entonces para un cuerpo negro, que absorbe y emite perfectamente la radiación $e_{\nu }=J(\nu ,T)$. Esta ecuación describe la potencia a una frecuencia específica de radiación, para todas las frecuencias, el poder total se obtiene integrando.

$e_{total}=\int _{0}^{\infty }e_{\nu }d\nu =a\sigma T^{4}$ (ec. 2)

Esquemática del problema de cuerpo negro

Joseph Stefan, en 1879, descubriría que la radiación total es proporcional a la cuarta potencia de la temperatura del cuerpo con una constante de proporcionalidad $\sigma =5.67\times 10^{8}{\frac {W}{m^{2}K^{4}}}$ llamada constante de Stefan-Boltzmann, y el parámetro $a$ sería una constante para radiadores no-ideales, pues para un cuerpo negro $e_{total}=a\sigma T=\sigma T$.

Densidad de energía espectral

Para analizar el problema de mejor manera, es más conveniente plantear una función de distribución $u(\nu ,T)$ que contenga información sobre la densidad de energía espectral (energía por unidad de volumen por unidad de frecuencia), en lugar de la función $J(\nu ,T)$ que nos dice sobre la potencia de radiación (potencia por unidad de superficie por unidad de frencuencia). En el caso del problema del cuerpo negro, donde se usa una cavidad oscura con un orificio por donde la radiación térmica puede escapar, la potencia por unidad de superficie por unidad de frecuencia de dentro de la cavidad es proporcional a su densidad de energía espectral. Podemos escribir que:

$J(\nu ,T)=u(\nu ,T)\alpha$ (ec. 3)

Donde $\alpha$ es la constante de proporcionalidad que mantiene la igualdad. Para encontrar el valor de esa constante podemos plantearnos lo siguiente:

Asumiendo que la luz de dentro de la cavidad se encuentra en equilibrio (la potencia absorbida por las paredes es igual a la emitida por ellas), y que la radiación es isotrópica y no-polarizada, la potencia de la luz en todo el ángulo sólido de la cavidad estará dada por:

$J(\nu ,T)4\pi$ (ec. 4)

Como tenemos una expresión de la potencia de esa superficie de luz, para tener su energía recordamos que la luz es isotrópica y será una esfera creciendo desde el centro a velocidad $c$, entonces:

$J(\nu ,T)\left[{\frac {W}{m^{2}f}}\right]{\frac {4\pi }{c}}\left[{\frac {s}{m}}\right]$

$J(\nu ,T){\frac {4\pi }{c}}\left[{\frac {J}{m^{3}f}}\right]$ (ec. 5)

Que efectivamente ahora está en unidades de densidad energética por unidad de volumen por unidad de frecuencia, recordando que $[W]=[Js]$. Esa es la constante de proporcionalidad que conecta las expresiones en la ecuación 3 entonces:

$J(\nu ,T)=u(\nu ,T){\frac {c}{4\pi }}$

Interpretación de la fórmula de Planck

Niveles discretos de energía dados por múltiplos de la constante de Planck

Para darle una interpretación física a su fórmula, Planck propondría que dentro del material constituyente del cuerpo negro habrían muchísimos "resonadores" (objetos de naturaleza desconocida, que luego resultarán ser los electrones). Estos "resonadores" serían cargas eléctricas microscópicas que vibran a una frecuencia relacionada a la de la luz emitida, para estar así en concordancia con la teoría electromagnética de Maxwell. Estos "resonadores" podrían sólo tener valores discretos de energía, múltiplos de $h$ (constante de Planck); además si emiten una onda electromagnética, su nivel energético bajaría al inmediato inferior, pero sólo perdiendo energía en múltiplos de la constante mencionada. La energía de los resonadores estaría dada por la siguiente expresión, y a diferencia de energía entre niveles sería de $hf$.

$E_{resonador}=nhf,n\in \mathbb {N} ,n=\{1,2,3...,\infty \}$