Diferencia entre revisiones de «Matemática II(UNI)»
+... |
+. |
||
| Línea 536: | Línea 536: | ||
| align="right" width="170" | '''Demostración:''' |
| align="right" width="170" | '''Demostración:''' |
||
|- |
|- |
||
| colspan="2" |Dado cualquier par de ángulos de un triángulo se tiene el tercero(propiedad angular 1). Por tanto se toma el segmento, por el <math>4^{to}</math> axioma, se construyen los ángulos que tiene en los extremos, y por el <math>1^{er}</math> axioma el nuevo par de lados, como no son paralelos, se cortan en un único vértice que es lo que se buscaba. |
| colspan="2" |Dado cualquier par de ángulos de un triángulo se tiene el tercero(propiedad angular 1), aunque es conocido como ALA. |
||
{| |
|||
|[[File:Postulado ALA 0.svg|200px]] |
|||
|[[File:Postulado ALA 1.svg|200px]] |
|||
|} |
|||
Por tanto se toma el segmento, por el <math>4^{to}</math> axioma, se construyen los ángulos que tiene en los extremos, y por el <math>1^{er}</math> axioma el nuevo par de lados, como no son paralelos, se cortan en un único vértice que es lo que se buscaba. |
|||
|} |
|} |
||
|- |
|- |
||
| Línea 545: | Línea 552: | ||
| align="right" width="170" | '''Demostración:''' |
| align="right" width="170" | '''Demostración:''' |
||
|- |
|- |
||
| colspan="2" |Se construye el ángulo con dichos lados, luego aplico el <math>2^{do}</math> axioma que me dice que por los extremos no comunes de los lados solo pasa una única recta que es lo que se buscaba. |
| colspan="2" | Se construye el ángulo con dichos lados, luego aplico el <math>2^{do}</math> axioma que me dice que por los extremos no comunes de los lados solo pasa una única recta que es lo que se buscaba. |
||
|} |
|} |
||
|- |
|- |
||
| valign="top" | |
| valign="top" |5. |
||
| En un triángulo se tiene que: |
| En un triángulo se tiene que: |
||
{| class="mw-collapsible wikitable {{#ifeq: {{{plegada|sí}}}|no||mw-collapsed|}}" width="100%" style="text-align:left; background-color:#fff;" |
{| class="mw-collapsible wikitable {{#ifeq: {{{plegada|sí}}}|no||mw-collapsed|}}" width="100%" style="text-align:left; background-color:#fff;" |
||
| Línea 554: | Línea 561: | ||
| align="right" width="170" | '''Demostración:''' |
| align="right" width="170" | '''Demostración:''' |
||
|- |
|- |
||
| Supongamos que tenemos un triángulo con dos lados iguales, lo único que tenemos que hacer es cosntruir el mismo triángulo sobre sí mismo con los lados intercambiados y veremos rápidamente que... . |
| colspan="2" | Supongamos que tenemos un triángulo con dos lados iguales, lo único que tenemos que hacer es cosntruir el mismo triángulo sobre sí mismo con los lados intercambiados y veremos rápidamente que... . |
||
|} |
|} |
||
|} |
|} |
||
Revisión del 11:05 20 ago 2015
El contenido de este curso viene definida por del reglamento de la Universidad Nacional de Ingeniería(UNI)(Perú):
- Geometría
- Trigonometría
Nociones básicas
Figura geométrica

Generalizando se puede definir figura geométrica como aquella que puede determinarse mediante puntos del plano o del espacio.
Ejemplo de figuras geométricas básicas
- Punto.
- Rectas o porciones de las mismas definidas por puntos.
- Circunferencias o porciones de las mismas definida por puntos.
- Cualquier gráfica.
- Plano o porciones del mismo definidas por o mediante las figuras anteriores.
También se puede definir figura geométrica como cualquier combinación de las anteriores figuras geométricas.
Representación, definiciones y notaciones
La representación y nominación de las figuras geométricas vienen estilizadas, en contra de los usos y ausencias de convenios en la Geometría, como:
El punto
|

Representado como un punto y entendida como un elemento sin extensión.[nota 2]
Su denominación se hace mediante letras mayúsculas: A, B, C, D, E, F, G, H, ...
La recta
|
Su representación debería ser una infinidad de puntos describiendo una línea recta que se extiende infinitamente es decir sin extremos pero debido a las limitaciones y costumbres locales se hace mediante un segmento con flechas en cada extremo para indicar su continuidad indefinida.

Notación: se hace mediante una "L" estilizada de una forma muy peculiar y seguida de subíndices a diferencia de la usada en el resto del mundo y es decir letras minúsculas:
- L1
Una segunda nominación de la recta se hace mediante dos puntos y un símbolo que emula una recta:
Ya que:
|
Diremos que dos rectas son paralelas cuando comparten las mismas orientaciones.
- Si dichas rectas comparten un punto diremos que son coincidentes.
Notación: si dos rectas son paralelas escribiremos L1 || L2 o si las dos paralelas están definidas por dos puntos, entonces se escribe o para el caso mixto L1
El plano
Representada como un paralelogramo y su nombre en letra mayúscula encerrada con un arco.
Notación: se usa la misma letra mayúscula seguida de un paralelogramo pequeño.
El segmento
Es una figura geométrica rectilínea que entendida como porción de una recta, delimitada por dos puntos, tiene la definición siguiente:
|
- El par de puntos que define cada segmento se llaman extremos del segmento.
Representado por una porción de recta con principio y fin, es decir, que une dos puntos.
Notación: Dado un segmento de extremos A y B, entonces se notará como
Longitud del segmento
Para medir longitudes se utilizan unidades de distancia establecidas previamente, podemos definirla como:
|
La longitud de se representa como o simplemente usando una letra minúscula: a, b, c, ...
El rayo
Es una figura geométrica rectilínea que entendida como una de las dos partes en que un punto divide a una recta, tiene la definición geométrica siguiente:
|
- El punto que determina el rayo se llama extremo.
- Todo rayo solo tiene un extremo.
- Se puede decir que el rayo se extiende hacia el infinito con un mismo rumbo u orientación
Llamaremos rayo opuesto al que con el mismo extremo se extiende en la otra orientación de la misma recta.
Notación: Dado el origen A y un punto cualquiera B de un rayo, entonces lo notaremos por
Ejercicios

Ángulos
En esta sección se detallan definiciones, propiedades, ejercicios y estrategias para trabajar con los ángulos.
El ángulo
Es una figura geométrica plana, entendida como dos rayos que comparten un mismo origen:
- El origen o punto en común se llama vértice.
- Los rayos son llamados lados.
Si esta fuera realmente la definición estricta del ángulo, entonces un triángulo no tendría ángulos por estar formado de segmentos y no de rayos.
Al entender el ángulo, como un concepto "local"[nota 6] al punto que comparten los dos rayos, aparecen diversos tipos de ángulos combinando rectas, rayos, segmentos y arcos de circunferencia arbitrariamente a los cuales llamaremos lados indistintamente.


Notación: Un ángulo queda determinado por tres puntos, en el orden siguiente de la imagen, donde es el vértice y por tanto ocupa la parte central.[nota 7]
Medida del ángulo
Dado un ángulo, al considerar que un lado está fijo y el otro tiene un movimiento de rotación articulado en su vértice, permite definir diferentes unidades de medidas de angulares, dividiendo una vuelta en diferentes partes, la más común son los grados sexagesimales.
- 1 vuelta = 360 grados.
- vuelta = 90 grado(un ángulo recto).
Notación: La medida de un ángulo se indica con una m delante del mismo y su valor se puede llamar a su vez por una letra griega:, , , ,
Clasificación de los ángulos
Considerando los ángulos menores que 180º tenemos la siguiente clasificación
| Según su medida | ||||||
|
Ángulos consecutivos
Dos ángulos son consecutivos si comparten el vértice y un lado.
Ángulos adyacentes
Se dice de los ángulos consecutivos que están a distinto lado del lado común.[nota 8]
Ángulos complementarios
Dos ángulos son mutuamente complementarios si sus medidas suman 90º.
- En estos casos diremos que un ángulo es el complemento del otro o complementario al otro.
- No es obligatorio que sean consecutivos.
Ángulos suplementarios
Dos ángulos son mutuamente suplementarios si sus medidas suman 180º.
- En estos casos diremos que un ángulo es el suplemento del otro o suplementario al otro.
- No es obligatorio que sean consecutivos.
Ejercicios

| 1. | Dada la representación de ángulos adjunta, se tiene que y
| ||||
| 2. | Dado el ejercicio anterior con y .
| ||||
| 3. | Dado el ejercicio inicial, si es 2 veces más grande que .
| ||||
| 4. | Dado el ejercicio inicial, nos dicen que .
| ||||
| 5. | Nos dicen que y que ¿como lo representamos?

| ||||
Ángulos opuestos por el vértice
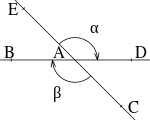
Diremos dos ángulos son mutuamente opuestos por el vértice un ángulo y el ángulo formado por los rayos opuestos del primero.
Supongamos que sus medidas son y , entonces se cumple que:
Para ir de las medidas de <EAC hasta <BAD, ambos de 180º, tenemos que restarle la medida y sumarle a la medida del primero, resultando:
al simplificar se tiene que |
El uso trigonométrico del ángulo puede dar una definición más general en cuanto a medidas de ángulo se refiere, por ejemplo, un ángulo de no tiene sentido en geometría, pues tal medida coincide con el concepto de línea recta y es decir que no tiene ángulo por ser recta. Luego también se tiene el concepto de orientación del ángulo que, en trigonometría, es la orientación horaria(negativa) y anti horaria(positiva) y para medir se tiene que fijar el lado a partir del cual se empieza a medir.
En la práctica viendo el ángulo como el giro o desviación de un cuerpo sobre una recta, podemos simplificar muchos problemas, véase las interpretaciones geométricas equivalentes:

|

|

|
Ejercicios

| 1. | Dada la representación de ángulos adjunta.
| ||||

| 2. | Un avión(en azul) ejecuta diferentes correcciones de su nuevo rumbo(en rojo).
| ||||
Ángulos de una secante a dos rectas
El interés recae en la secante a dos rectas sobre la cual aparecen dos vértices para distintos ángulos. Se prioriza el uso de secante a dos rectas paralelas pues si no son paralelas aparece un triángulo del cual ya se hablará en profundidad después.

Ángulos internos Son los ángulos que quedan comprendidos entre las dos rectas paralelas.
Ángulos externos Son los ángulos que no son internos.
Los siguiente ángulos no comparten vértice:
Ángulos alternos internos
Son los ángulos que quedan comprendidos entre las dos rectas paralelas y a distinto lado de la secante.
Ángulos alternos externos
Son los ángulos que no son internos y quedan a distinto lado de la secante.
Ángulos correspondientes
Son los ángulos que a un mismo lado de la secante, uno es externo y el otro interno.
Véase que el caso de recta secante a otras dos paralelas solo aparecen dos únicas medidas angulares que son suplementarias, esto permite saltar de unas rectas a otras que son sus paralelas cómodamente.
Ejercicios
 |
 |
| 1. | Un automóvil circula con dirección L0, luego gira a la derecha y toma la dirección L2, y luego con un giro a la izquierda se incorpora en una calle con dirección L1. Si nos dicen que y que L0 L1.
| ||||
| 2. | Un automóvil circula con dirección L0, luego gira a la izquierda y toma la dirección L2 en retroceso, y luego con un giro a la derecha se incorpora en una calle con dirección L1. Si nos dicen que y que L0 L1.
| ||||

| 3. | Un ejercicio de maniobras navales para un barco carguero, obliga al capitan a realizar una serie de giros para evitar obstaculos y seguir con el rumbo inicial, es decir que L0 L1, se le pregunta al capitán previamente:
| ||||

| 4. | Dadas dos pares de rectas paralelas, es decir, L0 L2 y L1 L3, si .
| ||||
Triángulos

Un triángulo son 3 puntos no colineales unidos mediante segmentos.
- A los 3 puntos se les llama vértice:
- A, B y C
- A sus 3 segmentos se les llama lados:
- , y
- Diremos que un vértice y un lado son opuestos si no están uno al lado del otro:
- opuesto de C, de A y de B.
- En cada vértice tiene 3 ángulos internos definidos por los lados contiguos.
- , y
- En cada vértice tiene 3 ángulos externos definidos por un lado contiguo y la prolongación del otro lado contiguo
- , y
Propiedades angulares del triángulo
Las siguiente propiedades se demuestran rápidamente con el método aprendido en la sección de ángulos.
Propiedades: Dado un triángulo se tiene:
- La suma de la medida de los ángulos internos es 180º.
- La suma de la medida de dos ángulos internos menos la del externo no adyacente es 0º.
- La suma de la medida de dos ángulos externos menos la del interno no adyacente es 180º.
- La suma de la medida de los ángulos externos es 360º.
Axiomas
- Dos rectas si se cortan, lo hacen en un único punto.
- Por dos puntos diferentes pasa una única recta.
- La línea recta tiene la longitud más corta entre dos puntos.
- Dado un punto sobre una recta y la medida de un ángulo, entonces el segundo lado del ángulo quedan determidados de forma única.
De estos axiomas se derivan las siguientes propiedades interesantes a nivel investigativo para la sección de congruencias. En resumen se persigue garantizar que un triángulo construido con los mismos datos sea el mismo.
Propiedades: En un triángulo se cumplen:
| 1. | La desigualdad triangular:[1]
| ||||||
| 2. | La desigualdades:
| ||||||
| 3. | Dado un triángulo mediante un lado y dos ángulos, entonces:
| ||||||
| 4. | Dado un triángulo mediante dos lados y el ángulo que forman, entonces:
| ||||||
| 5. | En un triángulo se tiene que:
| ||||||
Simetrías
Hallar una simetría de una figura geométrica consistirá en encontrar el eje de simetría, es decir los puntos de recta que equidistan a cada punto de la figura analizada y su punto simétrico.
- Se omitirá la simetría que pueda ter los conjuntos de puntos colineales(alineados) por la recta que los contiene.
- Dos puntos siempre tienen un eje de simetría, es la recta pasa por el punto medio de los dos puntos(por equidistancia a la recta).
- Un segmento tiene el mismo eje de simetría que el de sus dos extremos.
- Un ángulo tiene un eje de simetría que pasa por su vértice y contiene la bisectriz.
- Se puede considerar que una circunferencia tiene infinitos ejes de simetría y todos pasan por el centro de la misma.
- Se puede considerar que dos rectas paralelas tienen infinitos ejes de simetría perpendiculares a las mismas y un solo eje de simetría paralelo a dichas dos rectas y que transcurre entre ellas.
Ejercicios
Polígonos
Notas
- ↑ Este axioma figura en Los elementos, pero es más antiguo, ya que aparece con naturalidad en los escritos de las discusiones de las paradojas de Zenon como el de La dicotomía.
- ↑ La representación de un punto como el punto que tiene en común dos rectas que se cortan es la más recomendada y adecuada en otras áreas como el dibujo técnico.
- ↑ Aunque precisa sigue siendo una definición poco usada, lo normal en textos matemáticos puede ser algo como: donde donde es la recta sobre la que se intenta definir un segmento con A y B.
- ↑ La definición de distancia es lo primero que se hace para establecer longitudes o magnitudes, estas pueden tener distintas notaciones según el área de las matemáticas que se estudie: d(A,B) o .
- ↑ El nombre académico más conocido y usado es el de semirrecta habiendo dos tipos principalmente, una abierta y otra cerrada. El uso actual puede ser del tipo para el caso cerrado y para el caso abierto.
- ↑ Aquí local es usado como sinónimo de proximidad o cercanía en este caso al punto compartido por los dos rayos
- ↑ La orientación del ángulo también es importante para la trigonometría, para distinguir el sentido horario del anti horario . Otras notaciones también son válidas en otros textos como e incluso cuando no hay posibilidad de equivocarse.
- ↑ Hay importantes referencias en inglés y español que indican la obligatoriedad de que los lados no comunes pertenezcan a una recta, es decir, sean rayos opuestos de una recta. Pero hay otras referencias en francés que solo requieren un lado común y la intersección de las regiones angulares ha de ser dicho lado común.
- ↑ Para espacios métricos la desigualdad triangular no es una desigualdad estricta.












































































































