Definición de valor absoluto

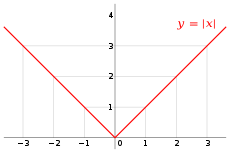
El valor absoluto es una función que representa la distancia de un punto al origen. Si tomamos un punto cualquiera x y este es positivo, la distancia de x al origen 0 es igual a x; si fuera negativo, la distancia de x al origen 0 es igual a -x.

Esto se debe a que una distancia no puede ser negativa, ya que no tendría sentido. Todas las distancias son positivas y por lo mismo, el valor absoluto de un número, que es una distancia, debe ser positivo.

De manera mas formal:

|a|={\begin{cases}\;\;\;a,&{\mbox{si }}a\geq 0\\-a,&{\mbox{si }}a<0\end{cases}}

Donde $|a|$ representa el valor absoluto o módulo de un número.

Definición alternativa

De forma alternativa, se puede definir el valor absoluto como $|a|={\sqrt {x^{2}}}$ , ya que al elevar x al cuadrado, el número quedara positivo, y al tomar su raíz cuadrada, tomaremos el mismo número x, ahora del lado positivo de la recta que es donde se halla el valor de la distancia.

|a| = máx {a, -a}; el valor absoluto de un número a ( que puede ser negativo, cero o positivo) es el máximo de los números a o -a. [[Archivo:Valor absoluto|miniaturista]

Referencias