Se presentan a continuación, ejercicios de cálculo organizados por tema, evaluando diferentes conceptos y con sus soluciones correspondientes.
Sean
a
∈
R
;
z
,
z
0
∈
C
.
Con
z
=
x
+
i
y
{\displaystyle a\in \mathbb {R} ;z,z_{0}\in \mathbb {C} .{\text{ Con }}z=x+iy}
z
z
¯
+
z
0
z
¯
+
z
0
¯
z
+
a
=
0
{\displaystyle z{\bar {z}}+z_{0}{\bar {z}}+{\bar {z_{0}}}z+a=0}
x
y
{\displaystyle xy}
Solución
Consideramos
z
0
=
b
+
i
c
{\displaystyle z_{0}=b+ic}
z
z
¯
=
|
z
|
2
=
x
2
+
y
2
{\displaystyle z{\bar {z}}={|z|}^{2}=x^{2}+y^{2}}
z
z
¯
+
z
0
z
¯
+
z
0
¯
z
+
a
=
0
x
2
+
y
2
+
(
b
+
i
c
)
(
x
−
i
y
)
+
(
b
−
i
c
)
(
x
+
i
y
)
+
a
=
0
x
2
+
y
2
+
b
x
+
c
y
+
i
(
c
x
−
b
y
)
+
b
x
+
c
y
−
i
(
c
x
−
b
y
)
+
a
=
0
x
2
+
y
2
+
b
x
+
c
y
+
i
(
c
x
−
b
y
)
+
b
x
+
c
y
−
i
(
c
x
−
b
y
)
+
a
=
0
{\displaystyle {\begin{array}{ccccccccc}z{\bar {z}}&+&z_{0}{\bar {z}}&+&{\bar {z_{0}}}z&+&a&=&0\\x^{2}+y^{2}&+&(b+ic)(x-iy)&+&(b-ic)(x+iy)&+&a&=&0\\x^{2}+y^{2}&+&bx+cy+i(cx-by)&+&bx+cy-i(cx-by)&+&a&=&0\\x^{2}+y^{2}&+&bx+cy\ {\cancel {+i(cx-by)}}&+&bx+cy\ {\cancel {-i(cx-by)}}&+&a&=&0\end{array}}}
⇒
x
2
+
y
2
+
2
b
x
+
2
c
y
+
a
=
0
{\displaystyle \Rightarrow x^{2}+y^{2}+2bx+2cy+a=0}
Fórmulas de la Circunferencia uso.
x
2
+
y
2
+
A
x
+
B
y
+
C
=
0
(
A
,
B
,
C
∈
R
)
⇒
{
A
=
2
b
B
=
2
c
C
=
a
{\displaystyle x^{2}+y^{2}+Ax+By+C=0\ (A,B,C\in \mathbb {R} )\Rightarrow \left\{{\begin{array}{l}A=2b\\B=2c\\C=a\end{array}}\right.}
A
2
4
+
B
2
4
−
C
=
(
2
b
)
2
4
+
(
2
c
)
2
4
−
a
=
4
b
2
4
+
4
c
2
4
−
a
=
b
2
+
c
2
−
a
=
|
z
0
|
2
−
a
{\displaystyle {\sqrt {{\frac {A^{2}}{4}}+{\frac {B^{2}}{4}}-C}}={\sqrt {{\frac {{(2b)}^{2}}{4}}+{\frac {{(2c)}^{2}}{4}}-a}}={\sqrt {{\frac {4b^{2}}{4}}+{\frac {4c^{2}}{4}}-a}}={\sqrt {b^{2}+c^{2}-a}}={\sqrt {{|z_{0}|}^{2}-a}}}
(
−
A
2
,
−
B
2
)
=
(
−
b
,
−
c
)
{\displaystyle \left({\frac {-A}{2}},{\frac {-B}{2}}\right)=(-b,-c)}
Fórmulas de la Circunferencia dice:
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}
(
a
,
b
)
{\displaystyle (a,b)}
r
{\displaystyle r}
x
2
+
y
2
+
2
b
x
+
2
c
y
+
a
=
0
⇔
x
2
+
2
b
x
+
y
2
+
2
c
y
+
b
2
+
c
2
=
−
a
+
b
2
+
c
2
⇔
(
x
+
b
)
2
+
(
y
+
c
)
2
=
b
2
+
c
2
−
a
{\displaystyle x^{2}+y^{2}+2bx+2cy+a=0\Leftrightarrow x^{2}+2bx+y^{2}+2cy+b^{2}+c^{2}=-a+b^{2}+c^{2}\Leftrightarrow (x+b)^{2}+(y+c)^{2}=b^{2}+c^{2}-a}
.Entonces la respuesta es, que es una circunferencia si se cumple la condición:
|
z
0
|
2
−
a
>
0
⇔
|
z
0
|
2
>
a
{\displaystyle {|z_{0}|}^{2}-a>0\Leftrightarrow {|z_{0}|}^{2}>a}
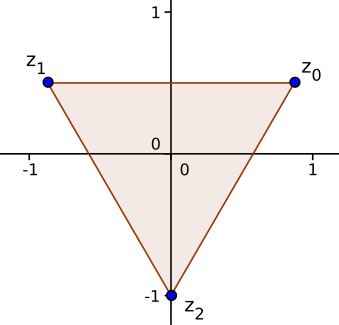
Considere las raíces cúbicas de
i
{\displaystyle i}
Dos de las raíces tiene la misma parte imaginaria.
Una de las raíces es imaginaria pura.
Las raíces se corresponden con los vértices de un triángulo equilátero con centro en el origen.
Sea
F
(
x
)
=
∫
π
x
e
t
3
+
s
e
n
(
t
)
d
t
{\displaystyle \displaystyle F(x)=\int _{\pi }^{x}{\frac {e^{t}}{3+sen(t)}}dt}
(
F
−
1
)
′
(
0
)
{\displaystyle (F^{-1})'(0)}
a
n
=
∫
0
π
4
c
o
s
(
x
)
−
s
e
n
(
x
)
(
s
e
n
(
x
)
+
c
o
s
(
x
)
)
n
+
1
d
x
y
b
n
=
1
n
−
a
n
, con
n
∈
R
{\displaystyle a_{n}=\displaystyle \int _{0}^{\frac {\pi }{4}}{\frac {cos(x)-sen(x)}{(sen(x)+cos(x))^{n+1}}}dx{\text{ y }}b_{n}={\frac {1}{n}}-a_{n}{\text{ , con }}n\in \mathbb {R} }
(
I
)
∑
n
=
1
+
∞
a
n
{\displaystyle (I)\ \displaystyle \sum _{n=1}^{+\infty }a_{n}}
(
I
I
)
∑
n
=
1
+
∞
b
n
{\displaystyle (II)\ \displaystyle \sum _{n=1}^{+\infty }b_{n}}
Proyecto de aprendizaje [ editar ] 
















![{\displaystyle z={\sqrt[{3}]{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc0f7ba3781c2eafd1cc98c035fbb36e9fb05806)



![{\displaystyle {\sqrt[{3}]{\rho }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/662ca99ae4378c110269ae502b432473af3b7452)