Oscilaciones armónicas en una dimensión

Introducción

Dada una variable física (distancia, ángulo), cuando las fuerzas que actúan son proporcionales y de sentido inverso a la separación de un valor de equilibrio, se producen oscilaciones armónicas de la variable física. Si la variable es l, la ecuación matemática que gobierna el mecanismo es

(1)${\frac {d^{2}l}{dt^{2}}}=-kl$

La solución a la ecuación diferencial es

(2)$l=Asen({\sqrt {k}}t)+Bcos({\sqrt {k}}t)$

El movimiento es periódico, ya que después de un tiempo $t={\frac {2\pi }{k}}$ se recupera la posición inicial.

Ley de Hooke

La ecuación (1) se aplica al comportamiento de muelles, cuando la desviación de la posición de equilibrio es pequeña. Si se considera la variable de posición x, se tiene entonces

(3)$x=Asen({\sqrt {k}}t)+Bcos({\sqrt {k}}t)$

Péndulo simple

Diagrama de las fuerzas que actúan en un péndulo simple.

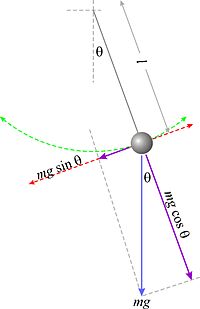
Al separar la masa de su punto de equilibrio, oscila a ambos lados de dicha posición, realizando un movimiento armónico simple. En la posición de uno de los extremos, se produce un equilibrio de fuerzas. Para derivar las ecuaciones pertenecientes a un péndulo gravitacional se deben hacer las siguientes hipótesis:

• Hilo flexible
• Hilo inextensible
• Hilo sin peso
• Punto material
• Movimiento en el vacío

La flecha azul representa la fuerza debida a la gravedad actuando sobre la masa. Las flechas violetas son la misma fuerza descompuesta en sus componentes paralelos y perpendiculares al movimiento instantáneo de la masa. La segunda ley de Newton

(4)$F=ma$

donde F es la fuerza actuando sobre la masa m, haciendo que acelere a metros por segundo cuadrado. Ya que la masa está obligada a moverse en un trazo circular verde, no hay necesidad de considerar ninguna otra fuerza que la responsable de aceleración instantánea paralela al movimiento instantáneo de la masa, la flecha violeta corta

(5)$F=mg\sin \theta =ma$

(6)$a=g\sin \theta$

La fuerza perpendicular, que mantiene la masa en estado de equilibrio con la tensión del hilo, es

(7)$F=mg\cos \theta$

Aceleración lineal $a$ por el axis rojo está relacionado con el cambio en el ángulo $\theta$ por la fórmula para encontrar el largo del arco

(8)$s=\ell \theta$

(9)$v={ds \over dt}=\ell {d\theta \over dt}$

(10)$a={d^{2}s \over dt^{2}}=\ell {d^{2}\theta \over dt^{2}}$

Esta aceleración no toma en cuenta que el ángulo $\theta$ está disminuyendo. Por lo tanto, la aceleración $a$ tiene que llevar un signo negativo:

(11)$\ell {d^{2}\theta \over dt^{2}}=-g\sin \theta$

Para oscilaciones pequeñas $\sin \theta \approx \theta$

Recuperandose la ecuación básica de las oscilaciones armónicas (1)

El periodo de oscilación de un péndulo simple restringido a oscilaciones de pequeña amplitud es

(13)$T=2\pi {\sqrt {\ell \over g}}$